LAB 3: Acceleration of Gravity on an Incline Plane

       Acceleration of Gravity on an Incline Plane

Purpose: The purpose of this lab was to find the acceleration of gravity by studying the motion of a cart on an incline.

Equipment used:    - windows based computer            - Logger pro software

                                   - Motion detector                               - Ballistic cart

                                   - Aluminum track                                - Wood blocks

                                   - Meter stick                                         - small carpenter level

Quick description:   In this lab we will used the computer to collect position (x) vs. time (t) data for a car accelerating on an inclined track. When comparing acceleration of the car moving up and down friction is eliminated. And we can find the acceleration of gravity only. If g is the acceleration due to gravity when car is in free fall, the acceleration along the track is g sinƟ and Ɵ is the angle of incline for the track.

Procedures we did:

1. connected labpro to the computer as well as the motion detector opened and loaded the Logger pro.

2. Inclined the track slightly by putting the wood friction block under the track approximately at the 50cm mark. Then used a bubble level or small carpenter level to make sure it was leveled from both sides. Then we found out what was the incline angel Ɵ by measuring the vertical and horizontal travel as shown in figure 1 below.
 

figure 1:shows how we solved for  Ɵ  when h=50 cm, x=49.95cm .  cosƟ=49.95cm/50cm  àƟ=cos^(-1)(49.95cm/50cm) àƟ=2.56˚

3. We then placed the detector at the upper end of the track facing down toward the bottom. Then we placed the car at the lower end and gave it a push up hill near the detector brining it no closer than 50cm to it. As shown in figure 2 below.

 figure 2

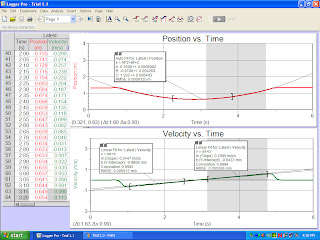
4. Started taking data on computer after car left hand. Meanwhile  we were observing both the position and the velocity graphs simultaneously. And properly labeld the graphs for position vs. time, velocity vs. time with titles and units etc. as shown in the figure 2 A.

                                                 Trial 1 using 2.56˚ three grpahs

                    

                                                                                                                          graph 1

                     graph 2

grpah 3

figure 2A show all 3 trials for small angle 2.56˚

   

 5.We found the accelerations, a1 and a2, of the car by determining the slope of the v vs. t curve for each portion of the motion going up and down. Then we selected a range  of time that represents the motion going up the incline. Then we selected analyze/curve fit and fit the selected portion to a linear function of time. The slope was the acceleration a1. Then we did the same thing for a2 and used                              g sinƟ= (a1+a2)/2   equation to determine g as in figure 3 A.

figure 3A: we solve for g=([.3447m/s^ (2)+.2995m/s^ (2)]/2)/ sin(2.56˚)=7.212m/s^ (2)

6. We did two more trials for the same incline. We then average are values and calculated are g and compared are results with the accepted value 9.80m/s^(2) as shown in figure 3B.
   figure 3B

                                                            SUMMARY TABLE  1^st trial using Ɵ=2.56˚

g experimental g=([a1+a2]/2)/sin(2.56˚)	Average = (1. +2. +3.)/3	Actual g=9.80 m/s^(2)	% difference = ([Experimental-actual]/actua)l x100%
1.       7.212 m/s^(2)	Average for	9.80 m/s^(2)	26.4%
2.       7.064 m/s^(2)	All  g experimental=	9.80 m/s^(2)	27.9%
3.       7.101 m/s^(2)	7.125 m/s^(2)	9.80 m/s^(2)	27.5%

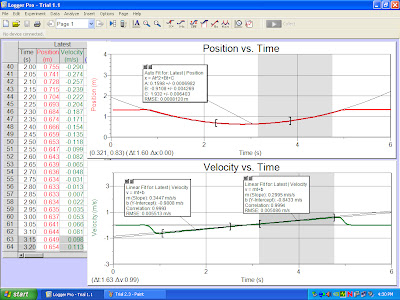
7. We repeated experiment (steps 2, 5 and 6) for the larger angle 5.73˚ by using larger block of wood to increase the angle of inclination of the track. As shown in figure 4A-figure  below.                
                                           Experiment 2 Larger angle

 

figure 4A :shows how we solved for  Ɵ  when h=50 cm, x=49.75 .  cosƟ=(49.75cm/5ocm)  àƟ=cos^(-1)(49.75cm/50cm) àƟ=5.73˚.

 figure 4B: For motion sensor setup we then placed the detector at the upper end of the track facing down toward the bottom. Then we placed the car at the lower end and gave it a push up hill near the detector brining it no closer than 50cm to it. As shown in picture above.

Figure 4C: shows three graphs for are 2nd experiment with the larger angel. We Included the appropriate labeling s title, and units etc.

 1 graph  2nd graph 3 rd graph

 figure 4D:

We did two more trials for the same incline. We then average are values and calculated are g and compared are results with the accepted value 9.80m/s^(2)

                                                            SUMMARY TABLE  2^st trial using Ɵ=5.73˚

g experimental g=([a1+a2]/2)/sin(5.73˚)	Average = (1. +2. +3.)/3	Actual g=9.80 m/s^(2)	% difference = ([Experimental-actual]/actua)l x100%
1.      1.   7.250 m/s^(2)	Average for	9.80 m/s^(2)	26.00%
2.      2.   7.227 m/s^(2)	All  g experimental=	9.80 m/s^(2)	26.25%
3.      3.   7.252 m/s^(2)	7.243 m/s^(2)	9.80 m/s^(2)	26.00%

  Unit analysis

    we solve for g=([.3447m/s^ (2)+.2995m/s^ (2)]/2)/ sin(2.56˚)=7.212m/s^ (2)

  Solving for Ɵ àƟ=cos^(-1)(49.95cm/50cm) àƟ=2.56˚

Solving for g experimental= ([7.255m/s^(2)+9.80255m/s^(2)]/2)/sin(5.73˚)= 7.250m/s^(2)

Solving for the average      = (2.250 m/s^(2)+7.225 m/s^(2)+7.252 m/s^(2))/3= 7.243 m/s^(2)

Solving %difference          = ( 7.250 m/s^(2)- 9.80 m/s^(2))/( 9.80 m/s^(2))x100%=26.00%

                                                 dimensional analysis

Solving for g experimental= ([m/s^(2)+m/s^(2)]/2)/sin(Ɵ  )=  m/s^(2)

Solving for the average      = ( m/s^(2)+ m/s^(2)+m/s^(2))/3=  m/s^(2)

Solving %difference          = ( m/s^(2)-  m/s^(2))/(  m/s^(2))x100% = %

 we solve for g=([m/s^ (2)+m/s^ (2)]/2)/ sin(Ɵ) = m/s^ (2)

  Solving for Ɵ=cos^(-1)(cm/cm) àƟ = x˚
                                

                                                 Units used in graph in si units

Time = s      Position = m    Velocity = m/s   g= m/s^(2)

                                                Conclusion

Based on the graph on what we talked in class are g experimental was on the average 7.243 m/s^ (2) and the actual g is 9.80 m/s^(2) meaning are percent error was 26% which is a lot. The problem was that are area measured was small therefore increasing are percent error was big. Had we used a larger are we would have a smaller percent error or percent difference as are teacher mentioned in class. But we did find the acceleration of gravity we were looking for.