INELASTIC COLLISION

INELASTIC COLLISIONS

Purpose:

To analyze the motion of two low friction carts during an inelastic collision and verify that the law of

conservation of linear momentum is obeyed.

Equipment:

Computer with Logger Pro software, lab pro, motion detector, horizontal track, two carts, 500 g

masses(3), triple beam balance, bubble level

Introduction:

This experiment uses the carts and track as shown in the figure. If we regard the system of the two

carts as an isolated system, the momentum of this system will be conserved. If the two carts have

a perfectly inelastic collision, that is, stick together after the collision, the law of conservation of

momentum says

              Pi = Pf

m1v1 + m2v2 = (m1 + m2)V

where v1 and v2 are the velocities before the collision and V is the velocity of the combined mass

after the collision.

 

Procedure:

1. Set up the apparatus as shown in Figure 1. Use the bubble level to verify that the track is as

level as possible. Record the mass of each cart. Connect the lab pro to the computer and the

motion detector to the lab pro. On the computer, start the Logger Pro software, open the

Mechanics folder and the Graphlab file.

2. First, check to see that the motion detector is working properly by clicking the Collect button to

start collecting data. Move the cart nearest the detector back and forth a few times while

observing the position vs time graph being drawn by the computer. Does it provide a

reasonable graph of the motion of the cart? Remember to be aware of unwanted reflections

caused by objects in between the motion detector and the cart. Also, position the carts so that

their velcro pads are facing each other. This will insure that they will stick together after the

collision.

3. With the second cart (m2) at rest give the first cart (m1) a moderate push away from the motion

detector and towards m2. Observe the position vs time graph before and after the collision.

What should these graphs look like? Draw an example:  m₁= 501.5g      m₂= 516.1g   

        the graph look like two parts of continuous increasing liner curves. The slope of first part should be lower than the second part. 

The slope of the position vs. time graph directly before and directly after the collision give the

velocity directly before and directly after the collision. To avoid the problem of dealing with

friction forces (Remember, we are assuming the system is isolated.), we will find the velocity of

the carts at the instant before and after the collision.

Is this a good approximation? Why or why not?

Its good we focused on change in the velocity after the collision. Comparing only before velocity and after velocity. We will have a error because of air resistance and friction.

For the velocity before the collision, select a very small range of data points just before the

collision. Avoid the portion of the curve which represents the collision. Choose

Analyze/Linear Fit. Record the slope (velocity) of this line. Repeat for a very small range of

data points just after the collision. Record this slope (velocity) as well.

Slope before =0.444

Slope after     =0.150

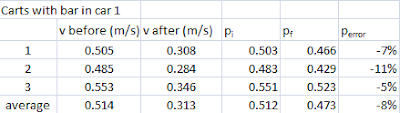
4. Repeat for two more collisions. Calculate the momentum of the system the instant before and

after the collision for each trial and find the percent difference. Put your results in an Excel data

table. Show sample calculations here:

 m₁= 501.5g     

     m₂= 516.1g 

    p_i = m₁× v_before +  m₂ × 0

      p_f = (m₁+ m₂) × v_after

      p_error = (p_f - p_i ) / p_f

5. Place an extra 500 g on the second cart and repeat steps 3 and 4. Sketch one representative

graph showing the position vs time for a typical collision. (What do velocity vs. time and

acceleration vs. time look like?

    m₁= 501.5g     
      m₂= 516.1g +495g= 1011.1g

  the acceleration is almost zero

 the acceleration is lower after than befor.

6. Remove the 500 g from the second cart and place it on the first cart. Repeat steps 3 and 4.

    m₁= 501.5g +495g= 996.5g   
        m₂= 516.1g

7. Find the average of all of the percent differences found above. This average represents your

verification of the law of conservation of linear momentum. How well is the law obeyed based

based on are results are percent difference was below 11% difference between pf and pi. 

on the results of your experiment? Explain.

8. For each of the nine trials above calculate the kinetic energy of the system before and after the

collision. Find the percent kinetic energy lost during each collision. Put this information in a

separate data table. Show sample calculations here:

9. Do a theoretical calculation for ÄK/K in a perfectly inelastic collision for the three situations:

1. a mass, m, colliding with an identical mass, m, initially at rest.

mv_b = 2mv_a     v_b = 2v_a 
          K = (1/2)×m×(v_b)^2
          ΔK = (1/2)×2m×(v_a)^2- (1/2)×m×(v_b)^2
          
          ΔK/K= -50%       
     

2. a mass, 2m, colliding with a mass, m, initially at rest.

  mv_b = 3mv_a     v_b = 3v_a 

          K = (1/2)×m×(v_b)^2

          ΔK = (1/2)×3m×(v_a)^2- (1/2)×m×(v_b)^2

          

          ΔK/K= -66.7%

3. a mass, m, colliding with a mass, 2m, initially at rest.

 2mv_b = 3mv_a     v_b = (3/2)v_a 

          K = (1/2)×2m×(v_b)^2

          ΔK = (1/2)×3m×(v_a)^2- (1/2)×2m×(v_b)^2

          

          ΔK/K= -33.3% 

Conclusions:

• What you learned

I learned that if there is no external force then the system is conserved. I also learned that momentum is = to mass x velocity. I also learned that momentum after collision is momentum impulse before + the new impulse.

• Sources of error we did not take into consideration air resistance and friction.  

• Compare your experimental numbers calculated in part 8 above with the results of your

theoretical calculations in part 9. In part 8 are percent energy lost form trial 4- 9 are close to theoretical values in part 9. From trial 1-3 there a little off maybe because it had no weight. Therefore it is influced by friction and air resistance more.